Parallelization Overhead for BBN

The theoretical speedup for the BBN as a function of N and W can be computed using the calculated values for the serial fraction, f, given in table 5.2. When this is done, the results compare quite poorly with the observed speedups tabulated in table 5.1. This indicates that the parallelization overhead cannot be ignored, and one needs to include a non-zero $\Delta\tau$ in the equation for speedup i.e., equation (5.5). Let us start with equation (5.5), and assume that $\Delta\tau$ can be modeled as follows:

$${\Delta\tau} {\approx} {\alpha{{N-1}\over{\nu}}}\;\;\;,$$ (118)

where $\alpha$ is a constant. This model assumes that the increase in time due to parallelization is proportional to the increase in the number of processors and inversely proportional to the processor speed $\nu$. Substituting equation (5.15) into equation (5.5) and using the results from equations (5.7) to (5.9), we find the following expression for speedup:

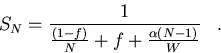$${S_N} = {{1}\over{{{(1-f)}\over{N}}+f+{\alpha{(N-1)}\over{W}}}}\;\;\;.$$ (119)

This expression for speedup is used to find values of $\alpha$ that would force the predicted speedups to match the observed speedups given in table 5.1. These ``required'' values of $\alpha$ show a trend in $\alpha$ somewhat independent of W but nearly linear with N, the number of processors. Therefore, $\alpha$ was modeled as follows:

$${\alpha} {\approx} 0.0006{{N}\over{116}}\;\;\;.$$ (120)

This expression is linear with N and the constant 0.0006 appears due to the fact that the required $\alpha$ was approximately 0.0006 for N=116, somewhat independent of W. Of course, this implies that the overhead term $\Delta\tau$ is not linear in N but quadratic:

$${\Delta\tau} {\approx} {{0.0006}\over{.116\nu}}N(N-1)\;\;\;.$$ (121)

This O(N²) dependence may be due to memory contention resulting from the BBN implementation of the message passing system, LMPS, which relies on the shared memory features of the BBN.

This expression for $\alpha$ in equation (5.17) was then used in equation (5.16) to predict the speedups for the five different workloads and the number of processors varying from 1 to 116. The results are shown in figure 5.3. The plots include the observed speedups from table 5.1 for comparison. It is clear that this simple model, which uses two empirical parameters (f and $\alpha$), predicts the behavior of the BBN very well over a wide range of numbers of processors and workloads.

 

Figure: Observed and Predicted Speedups for BBN.

This model explains the behavior of the performance curves. As the workload, W, increases, linear speedups result even for the largest number of processors because the serial fraction, f, is inversely proportional to W, and equation (5.16) shows that the speedup becomes linear in N as f decreases and W increases. For small workloads, f increases and S_N goes to zero, except for a small numbers of processors where the effect of the parallelization overhead vanishes, resulting again in a linear behavior of speedup S_N.