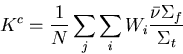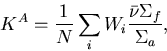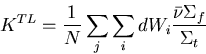Monte Carlo K Estimators

An estimator is a specific function of the random samples, of a random variable, that statistically represents a true unknown mean. If x is a random variable with an associated distribution and an unknown mean, then the function X(x₁, x₂, x₃,...,x_n) is an estimator of the unknown mean. The set {x₁, x₂, x₃,...,x_n} consists of n independent random samples selected from the probability density distribution of x. A good estimator should be unbiased, consistent, and efficient [Bow72]. An estimator is unbiased if its expected value equals the true mean, 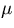$\mu$, i.e.,

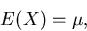$$E(X) = \mu,$$ (17)

for all X. Consistency applies to a single sample where the sample size, n, becomes large. An estimator is consistent if it approaches, in a statistical sense, the true mean as n gets large. An efficient estimator is the one, among a group of unbiased estimators, that produces the minimum variance for a given sample size n. Mathematical expression for each of the three estimators of K are given here. We use the superscripts C, A and TL for the collision, absorption and track length estimators respectively.

Collision Estimator:
The collision estimate of K for an active batch is:

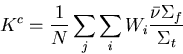$$K^c = \frac {1}{N} \sum\limits _{j} \sum\limits _{i} W_i {{{ \bar \nu {\Sigma_f}} \over{ {\Sigma_t}}}}$$ (18)

where,
i = all collisions for a particle in regions where fission is possible;
j = all source particles for a batch;
N = number of source particles for a batch; and
W_i = weight of particle entering collision.
Then the quantity 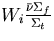$W_i {{{ \bar \nu {\Sigma_f}} \over{ {\Sigma_t}}}}$ in equation (2.18) is the expected number of neutrons to be produced from a fission process in collision i. Hence K^c is the mean number of fission neutrons produced per generation (or batch).

Absorption Estimator:
The absorption estimator of K for an active batch:

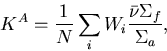$$K^{A} = \frac {1}{N} \sum\limits _{i} W_i {{\bar \nu {\Sigma_f}} \over{{\Sigma_a}}},$$ (19)

where,
i = an analog capture event; and
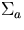${\Sigma_{a}}$ = macroscopic absorption cross section.

Track Length Estimator:
The track length estimator for K is given by,

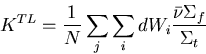$$K^{TL} = \frac {1}{N} \sum\limits _{j} \sum\limits _{i} d W_i \frac {\bar \nu {\Sigma_f}}{\Sigma_t}$$ (20)

where,
d = track length segment;
i = all track length segments,d, for a particle; and
j = all source particles for a batch.
In criticality calculations at the end of each batch (or fission generations) an estimate of K is produced by each of these three estimators. The final K estimator of each type is the average over many batch K estimates. Recent studies [Urb95a] have suggested that a combination of the three estimators to be the best K estimate available. In our research work we have used the collision estimator for all criticality and perturbation calculations. It should be emphasized that for Monte Carlo criticality calculations, the final result is not a point estimate of K, but rather a confidence interval.